数据挖掘之聚类分析总结（建议收藏）

聚类分析是按照个体的特征将他们分类，让同一个类别内的个体之间具有较高的相似度，不同类别之间具有较大的差异性

聚类分析属于无监督学习

聚类对象可以分为Q型聚类和R型聚类

Q型聚类：样本/记录聚类 以距离为相似性指标 (欧氏距离、欧氏平方距离、马氏距离、明式距离等)

R型聚类：指标/变量聚类 以相似系数为相似性指标 (皮尔逊相关系数、夹角余弦、指数相关系数等)

K-Means划分法

层次聚类法

DBSCAN密度法

K表示聚类算法中类的个数，Means表示均值算法，K-Means即是用均值算法把数据分成K个类的算法。

K-Means算法的目标，是把n个样本点划分到k个类中，使得每个点都属于离它最近的质心(一个类内部所有样本点的均值)对应的类，以之作为聚类的标准。

K-Means算法的计算步骤

取得k个初始质心：从数据中随机抽取k个点作为初始聚类的中心，来代表各个类

把每个点划分进相应的类：根据欧式距离最小原则，把每个点划分进距离最近的类中

重新计算质心：根据均值等方法，重新计算每个类的质心

迭代计算质心：重复第二步和第三步，迭代计算

聚类完成：聚类中心不再发生移动

基于sklearn包的实现

导入一份如下数据，经过各变量间的散点图和相关系数，发现工作日上班电话时长与总电话时长存在强正相关关系。

选择可建模的变量并降维。

cloumns_fix1 = ['工作日上班时电话时长', '工作日下半时电话时长',  

    '周末电话时长', '国际电话时长', '平均每次通话时长'] 

#数据降维 

pca_2 = PCA(n_components=2) 

data_pca_2 = pd.DataFrame(pca_2.fit_transform(data[cloumns_fix1])) 

通过sklearn包中的K-Means方法构建模型。

#绘制散点图查看数据点大致情况 

plt.scatter(data_pca_2[0],data_pca_2[1]) 

#预计将数据点分类为3类 

kmmodel = KMeans(n_clusters=3) #创建模型 

kmmodel = kmmodel.fit(data[cloumns_fix1]) #训练模型 

ptarget = kmmodel.predict(data[cloumns_fix1]) #对原始数据进行标注 

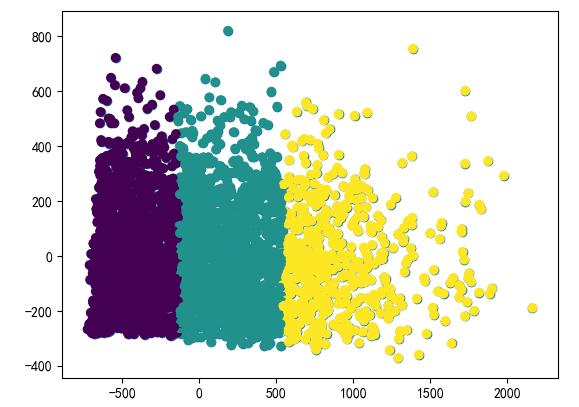
pd.crosstab(ptarget,ptarget) #交叉表查看各个类别数据的数量 

plt.scatter(data_pca_2[0],data_pca_2[1],c=ptarget)#查看聚类的分布情况。

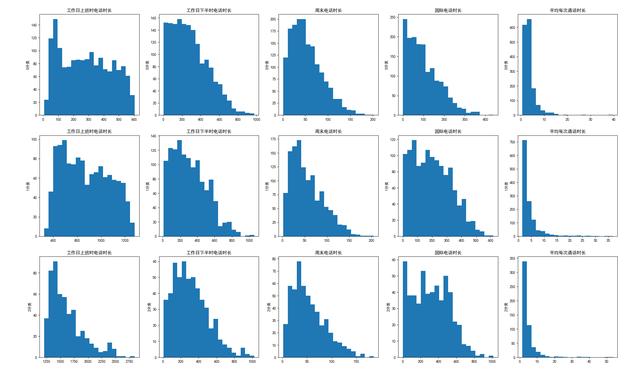
最后，可以通过直方图查看各聚类间的差异。

#查看各类之间的差异 

dMean = pd.DataFrame(columns=cloumns_fix1+['分类']) #得到每个类别的均值 

data_gb = data[cloumns_fix1].groupby(ptarget) #按标注进行分组 

i = 0 

for g in data_gb.groups: 

    rMean = data_gb.get_group(g).mean()  

    rMean['分类'] = g; 

    dMean = dMean.append(rMean, ignore_index=True) 

    subData = data_gb.get_group(g) 

    for column in cloumns_fix1: 

        i = i+1; 

        p = plt.subplot(3, 5, i) 

        p.set_title(column) 

        p.set_ylabel(str(g) + "分类") 

        plt.hist(subData[column], bins=20) 

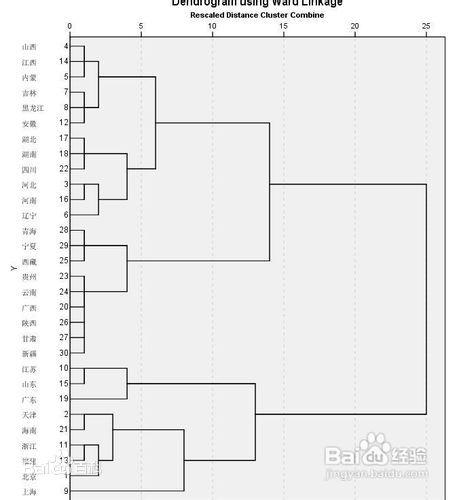
层次聚类算法又称为树聚类算法，它根据数据之间的距离，透过一种层次架构方式，反复将数据进行聚合，创建一个层次以分解给定的数据集。层次聚类算法常用于一维数据的自动分组。

层次聚类算法是一种很直观的聚类算法，基本思想是通过数据间的相似性，按相似性由高到低排序后重新连接各个节点，整个过程就是建立一个树结构，如下图：

层次聚类算法的步骤：

每个数据点单独作为一个类

计算各点之间的距离(相似度)

按照距离从小到大(相似度从强到弱)连接成对(连接后按两点的均值作为新类继续计算)，得到树结构

基于sklearn包的实现

使用K-Means聚类案例中的数据。

cloumns_fix1 = ['工作日上班时电话时长', '工作日下半时电话时长',  

    '周末电话时长',  

    '国际电话时长', '平均每次通话时长'] 

linkage = hcluster.linkage(data[cloumns_fix1], method='centroid') #中心点距离计算，得到矩阵 

linkage = scipy.cluster.hierarchy.linkage(data, method='single') 

method 类距离计算公式有三种参数：

single 两个类之间最短距离的点的距离

complete 两个类之间最长距离的点的距离

centroid 两个类所有点的中点的距离

#层次聚类绘图 

hcluster.dendrogram(linkage)  #不设置参数时会将所有点做为一个基础的类进行树结构的绘制 

#由于数据量大，限制类的个数,保留12个节点，有括号表示副节点，括号内的数字为该节点内部包含的子节点 

（编辑：应用网_阳江站长网）

【声明】本站内容均来自网络，其相关言论仅代表作者个人观点，不代表本站立场。若无意侵犯到您的权利，请及时与联系站长删除相关内容!